1 Models lineals

Els models que s'exposaran en aquesta unitat són lineals en el següent sentit: la variació amb el temps d'una variable serà lineal respecte a la pròpia variable

$$\frac{dQ}{dt} = a Q + C.$$

L'objectiu és trobar una funció $Q(t)$ que descrigui la dependència de la variable respecte el temps, tot i que a vegades en tindrem prou amb conèixer algunes propietats de la solució, com, per exemple, el comportament a llarg termini.

Si tenim vàries variables, el model serà lineal sempre i quan la variació d'una variable depengui linealment de les variables del sistema. Per exemple, en el cas de 3 variables

$$\begin{eqnarray*} \frac{dQ_1}{dt} &=& a_{11} Q_1 + a_{12} Q_2 + a_{13} Q_3 + C_1... ... \frac{dQ_3}{dt} &=& a_{31} Q_1 + a_{32} Q_2 + a_{33} Q_3 + C_3 \end{eqnarray*}$$

Naturalment, algunes d'aquestes constants poden ser igual a zero. Aquest tan sols és el cas lineal més general possible per a tres variables.

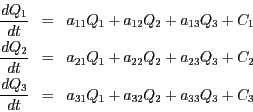
Una de les propietats del sistema anterior és que es pot expressar de manera compacta mitjançant operacions matricials

$$\frac{d}{dt} Q_i = \sum_j a_{ij} Q_j + C_i$$

la qual cosa pot ser interessant a l'hora de resoldre el model mitjançant l'ordinador. La notació és l'habitual, tant en àlgebra com en anàlisi matemàtica.

Ha arribat, però, el moment de fixar idees i adaptar aquesta notació al nostre propòsit. En aquesta unitat volem modelitzar la transferència d'una substància d'un lloc a l'altre. Aquesta substància pot ser un element molt concret, com ara un radionúclid, o pot ser un tipus genèric de material, per exemple matèria orgànica o nutrients.

$Q_i$ representarà la quantitat (segons el model també pot ser una concentració) d'aquesta substància que es troba a dins d'un compartiment $i$. El significat físic d'aquests compartiments depèn del model. Si estem estudiant el metabolisme, els compartiments representaran els òrgans de l'animal. En el cas de les cadenes tròfiques, poden representar éssers vius sencers. En qualsevol cas, es tracta d'una abstracció que deliberadament passa per alt els detalls referents al seu funcionament.

També donarem per suposada l'existència d'un medi que, per definició, contindrà tot el que no sigui a dins d'un compartiment. Això fa que la quantitat de substància al medi no sigui quantificable, ja que n'hi haurà molta més al medi que en qualsevol dels compartiments. Tan sols podrem quantificar els intercanvis del medi amb els compartiments.

Ens serà útil una notació que posi de manifest quina part de la variació d'una quantitat es deguda a la transferència de substància d'un compartiment a l'altre, quina es deu a intercanvis amb el medi i quina desapareix per la pròpia desintegració de la substància.

Considerarem que la transferència de matèria entre dos llocs diferents té lloc a través de fluxos. Cada flux serà proporcional a la quantitat a un dels dos compartiments i el considerarem positiu quan sigui aquesta quantitat la que perdi substància.

Segons això, hi haurà un flux del compartiment $i$ al compartiment $j$. Degut a aquest flux, el lloc $i$ perd una quantitat $k_{ij}Q_i$ per unitat de temps. Aquesta quantitat és la que guanya el lloc $j$ a causa d'aquest flux. Simultàniament, hi ha un altre flux, de $j$ a $i$, que transfereix una quantitat $k_{ji}Q_j$ per unitat de temps.

Part de la substància no es transfereix d'un lloc a l'altre. Això pot ser degut a que hi hagi una aportació del medi, una pèrdua al medi o a que la substància no sigui inert i vagi desapareixent amb el temps. Suposarem que tant la quantitat de substància desintegrada a $i$ com les pèrdues del compartiment $i$ cap al medi són proporcionals a la quantitat total que hi ha a aquest compartiment. En canvi, considerarem que les aportacions del medi són constants. La quantitat perduda al compartiment $i$ que no va a parar a altres compartiment és doncs, per unitat de temps

$$\lambda Q_i + k_{ii} Q_i - C_i.$$

Les constants $k$ i $C$ poden ser negatives, si així ho requereix el problema que estem estudiant. $\lambda$ acostuma a ser una constant coneguda, característica del material i és igual a zero en el cas de materials inerts.

Amb aquesta nova notació podem escriure el sistema anterior com

$$\begin{eqnarray*} \frac{dQ_1}{dt} &=& - (\lambda + k_{11} + k_{12} + k_{13}) Q_1... ... + k_{23} Q_2 - (\lambda + k_{31} + k_{32} + k_{33}) Q_3 + C_3 \end{eqnarray*}$$

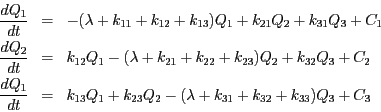
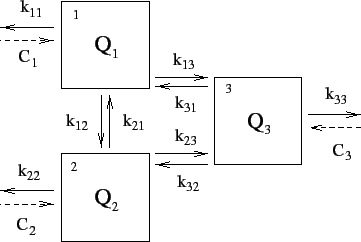
El millor d'aquesta nova notació és la facilitat per representar-la gràficament. Dibuixarem cada compartiment $i$ com una capsa, els fluxos com a línies contínues i les aportacions constants com a línies discontínues. La representació gràfica del sistema es pot veure a la Figura 1.

Figura 1: El model lineal més general possible per a la transferència d'una substància entre tres llocs diferents

Per practicar, pots fer les activitats 1 i 2.

Aquests models poden tendir cap a un estat estacionari o, en altres paraules, el sistema pot tenir un punt fix. En aquest estat les quantitats $Q_i$ no varien i, en conseqüència, les seves derivades són iguals a zero. Si notem com a $Q_i^*$ el valor de les variables a l'estat estacionari, el següent sistema algebraic

$$\begin{eqnarray*} C_1 &=& (\lambda + k_{11} + k_{12} + k_{13}) Q_1^* - k_{21} Q_... ...1^* - k_{23} Q_2^* + (\lambda + k_{31} + k_{32} + k_{33}) Q_3^* \end{eqnarray*}$$

ens permet trobar el punt fix per a uns valors donats de $k_{ij}$ i $C_i$. En el cas que sigui incompatible entendrem que el model no tendeix cap a l'equilibri.

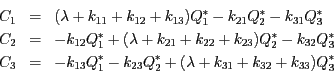
Quan estudiem un sistema real ens trobem gairebé sempre que ja és en equilibri. En aquests casos ens resultarà més fàcil mesurar experimentalment les quantitats a l'estat estacionari $Q_i^*$ i les aportacions del medi. El problema és l'invers de l'anterior ja que ara les incògnites són les constants $k_{ij}$ del sistema. Cal tenir en compte que aquest problema tan sols es pot resoldre, sense fer aproximacions addicionals, quan el nombre de fluxos és igual al nombre de compartiments del model.