- Troba els punts fixos del sistema d'equacions de
recurrència
i discuteix la seva estabilitat.
- Dues espècies que competeixen per una mateixa font
de recursos estan descrites pel sistema d'equacions d'equacions de
recurrència
Normalitza aquest sistema d'equacions.
- Consulta un llibre de Zoologia o una enciclopèdia.
Amb aquesta informació, enuncia 5 parelles d'espècies que tinguin una
relació presa-depredador.
- El següent sistema d'equacions normalitzades descriu
la relació entre una presa i el seu depredador
En un cert instant de temps, s'assoleixen els valors 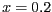 i
i 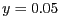 .
Si per normalitzar el depredador s'ha escollit
.
Si per normalitzar el depredador s'ha escollit 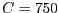 i es coneix que la
capacitat de la presa es
i es coneix que la
capacitat de la presa es 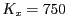 , quin és el nombre d'exemplars de cada
espècie? Quant val la probabilitat
, quin és el nombre d'exemplars de cada
espècie? Quant val la probabilitat 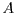 de que un depredador capturi una
presa en el transcurs d'un torn?
de que un depredador capturi una
presa en el transcurs d'un torn?
- Escriu el sistema d'equacions diferencials sense
normalitzar que correspon a aquest sistema d'equacions normalitzades
si les capacitats de les espècies són 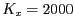 i
i 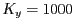 .
.
- Si normalitzem aquest sistema d'equacions
diferencials, que descriuen la interacció entre una presa i un depredador,
quins són els paràmetres 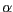 i
i 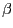 que en resultarien? Escriu un
sistema d'equacions de recurrència que en sigui equivalent, suposant que
les unitats de temps de les equacions anteriors són anys. Especifica quin
valor de
que en resultarien? Escriu un
sistema d'equacions de recurrència que en sigui equivalent, suposant que
les unitats de temps de les equacions anteriors són anys. Especifica quin
valor de 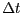 has escollit.
has escollit.
- Realitza les activitat descrites al guió de pràctiques d'aquesta
unitat.
Taller de simulació medi ambiental
2009-02-27

