- Els paràmetres
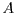 i
i 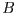 que corresponen al sistema normalitzat
que corresponen al sistema normalitzat
són, si 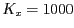 i
i 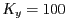 ,
,
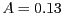
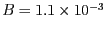
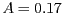
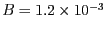
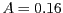
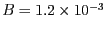
- Cap de les anteriors
- Els paràmetres
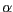 i
i 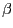 del sistema
del sistema
un cop normalitzat són (si emprem la mateixa normalització per a les dues
variables)
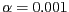
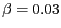
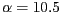
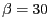
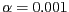
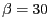
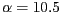
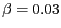
- El sistema d'equacions diferencials
té com a punts fixos
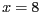
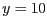
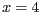
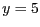
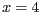
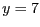
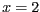
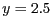
- Si volem normalitzar la variable
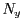 del següent sistema
del següent sistema
caldrà utilitzar la quantitat
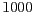
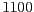
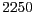
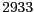
- En un model presa-depredador hem aplicat la mateixa normalització
per a la presa que per al depredador. Si la capacitat de la presa és
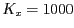 ,
, 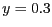 vol dir
vol dir
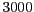
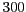
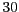
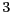
- Si en un model presa-depredador continu
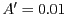 , llavors en un
model discret a on
, llavors en un
model discret a on 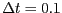 ,
, 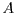 valdrà
valdrà
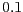
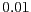
Taller de simulació medi ambiental
2009-02-27

