En el cas d'un llac, s'ha de treballar una mica més per poder obtenir la
concentració de contaminant. Considerarem un llac com el de la
Fig. 3,
Figura 3:
Paràmetres per calcular la concentració
d'un contaminant a un llac
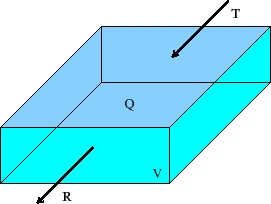 |
amb un abocament d'intensitat 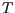 , un volum
, un volum 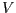 i un cabal de sortida
i un cabal de sortida 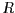 .
Si anomenem
.
Si anomenem 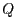 a la quantitat de contaminant i
a la quantitat de contaminant i 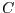 a la seva concentració,
està clar que la relació entre ambdues magnituds vindrà donada per
a la seva concentració,
està clar que la relació entre ambdues magnituds vindrà donada per
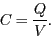 |
(4) |
Pensem ara per quins motius varia la quantitat de contaminant 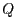 . Per una
banda tenim una variació deguda a l'abocament
. Per una
banda tenim una variació deguda a l'abocament
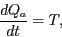 |
(5) |
una altra deguda a la quantitat de contaminant que es perd a través del flux
de sortida
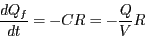 |
(6) |
i una altra deguda a la descomposició del contaminant
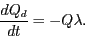 |
(7) |
Sumant aquestes equacions terme a terme obtenim la següent equació diferencial
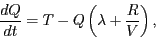 |
(8) |
la solució de la qual és
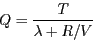 |
(9) |
o aplicant l'Eq. 4, si es prefereix en termes de la concentració,
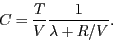 |
(10) |
Per fixar idees, fes les activitat 3, 4 i
5.
Taller de simulaciķ medi ambiental
2009-02-27


![]() . Per una
banda tenim una variació deguda a l'abocament
. Per una
banda tenim una variació deguda a l'abocament